A few weeks ago, the leak of President Jokowi's vaccination certificate became trending in cyberspace for days. The leak of the vaccination certificate was due to Jokowi's National Identity Number (NIK) being leaked by the KPU, which was intentionally leaked with the President's permission when he was running as a presidential candidate.
Actually, I'm still searching myself, what's really the problem if NIK is leaked? Isn't NIK easy to guess anyway? If calculated using combinatorial formulas, the 16-digit numbers in NIK would produce combinations or 100 quadrillion.
Wait, hold on. If examined carefully, it turns out it's not that many. In fact, the 16-digit NIK is divided into seven parts, with each part representing your demographic data attributes. Here's the breakdown.
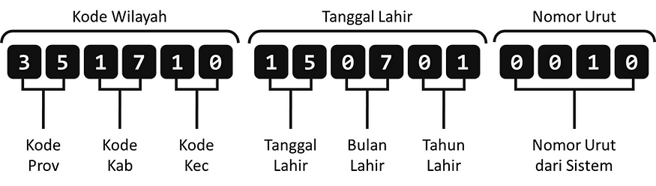
I was apparently wrong in guessing that the first 6 digits had or 10 million combinations. These six digits consist of: the first 2 digits are the province code, the second 2 digits are the regency code, the third 2 digits are the district code. From this information, the number of possibilities for the first 6 digits equals the number of districts in Indonesia. According to data from BPS, there were 7,252 districts in Indonesia in 2019.
The number 7,252 might be very-very much smaller than the previous estimate of 10 million combinations. However, if this number is tried one by one on the PeduliLindungi dashboard, it would take a long time. The only very easy way is to know the target's domicile. Public figures like Jokowi, we all certainly know his domicile. Our close friends can also become sweet targets. Besides that, distant people can also be targeted by digging information from their social media. So, don't carelessly share personal information. Oh yes, province codes, regency/city codes, up to district codes exist and are indeed disseminated to facilitate population data collection.
Birth Date and Gender (4 digits)
Previous assumption would certainly produce combinations for these 4 digits. Upon closer examination, the first 2 digits show the birth date and the next 2 digits show the birth month. If female, 40 is added to the birth date. Therefore, these 4 digits will produce combinations obtained from multiplying the number of days in a year (365 days) by 2 genders. Similar to the technique for guessing the first 6 digits, these 4 digits can also be easily guessed when we can find out the target's birth date. Close friends can certainly be easily guessed. For public figures, just search for their biodata on Google. For other people? Just search on social media, Facebook for example. Hey, those who still have Facebook accounts should immediately secure their birthday information.
Birth Year (2 digits)
From BPS data in 2020, life expectancy for males reaches 69.59 years while females 73.46 years. Let's assume on average the oldest people still alive today are 70 years old or born in 1950. So, for these 2 digits showing birth year, there will only be possible combinations. Same as before, birth year can also be easily found on the internet, on the target's social media.
Sequential Number (4 digits)
If the previous twelve digits are the same, meaning they have the same domicile down to the district level, same gender, and same birth, then the differentiator is these last 4 digits. Don't worry, these last 4 digits won't reach 9999. Cases of similarity in these twelve digits will depend on the area's density. If the area is dense, it might reach 100 possibilities; if the area is quiet, at most 10. For these last 4 digits, we can't guess anymore. The only thing that can be done is to try them directly on the PeduliLindungi dashboard. I will take 20 possible combinations for the last 4 digits for the final calculation.
Combinatorial Analysis
Based on the breakdown of the 16-digit NIK, the number of possible NIK combinations that can be guessed if the target is not someone we know at all and the target's digital footprint is secure (we know the target doesn't use Facebook) is calculated as follows:
Example 1: Guessing Mr. X with no information at all
NIK Combinations = combinations
Example 2: Guessing Mr. X if only gender is known
NIK Combinations = combinations
What if biodata has already been spread? Domicile and birth date have been shared on Facebook profile. Ah, and you've forgotten the password.
Example 3: Guessing Mr. X if domicile, gender, and birth date are known
NIK Combinations = combinations
The President's NIK leak isn't just about one person's privacy—it exposes a systemic vulnerability in Indonesia's national identity infrastructure. The mathematical analysis shows that NIKs are far from the secure identifiers they appear to be.
This case study demonstrates how combinatorial analysis can reveal hidden vulnerabilities in seemingly complex systems. When designing security systems, it's crucial to consider not just theoretical security, but practical attack vectors that leverage publicly available information.
The lesson here extends beyond NIKs: any system that encodes predictable information into identifiers creates potential security vulnerabilities. True security requires unpredictability, not just complexity.
Without attempting to actually use your NIK, you can practice this for yourself. If successful, try guessing your parents', your partner's, or your close friends' NIK. Happy trying—and stay secure!